| در تحليل جريان آب در آبراهههاى روباز از مفهوم انرژى مخصوص استفاده مىشود. بر حسب تعريف انرژى مخصوص در هر نقطه از يک آبراهه برابر است با مجموع عمق آب و ارتفاع نظير سرعت (بار سرعت):
|
|
| (معادله ۱۶): |
E = y + v2/2g |
|
|
| که در آن:
|
|
| E= انرژى مخصوص بر حسب متر است.
|
|
|
| چنانچه دبى آبراهه Q باشد در مقطع مستطيلى با عرض b مقدار دبى در واحد عرض آبراهه (q) خواهد بود با:
|
|
| |
|
| که در آن:
|
|
| q= دبى در واحد عرض آبراهه است (m3/s.m)
|
|
|
| در اينصورت سرعت جريان عبارت است از:
|
|
| (معادله ۱۸): |
v = Q/A = q(b) / y(b) = q/y |
|
|
| اگر در معادله (۱۶) بهجاى v مقدار معادل آن را از معادله (۱۸) قرار دهيم خواهيم داشت:
|
|
| (معادله ۱۹): |
E = y + q2 / y2(2g) |
|
|
| و لذا :
|
|
| (معادله ۲۰): |
(E-y) y2 = q2 / 2g |
|
|
| در جريانهاى ماندگار جزء سمت راست مقدار ثابتى است.
|
|
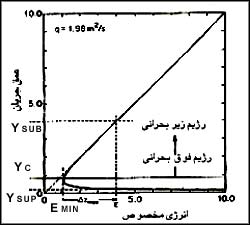
| اگر به ازاء مقدار ثابت q معادله ۲۰ را در يک دستگاه مختصات رسم کنيم شکلى مطابق شکل (منحنى انرژى مخصوص به ازاء مقدار ثابت دبي) بهدست مىآيد. اين شکل (منحنى انرژى مخصوص به ازاء مقدار ثابت دبي) به ازاء q=1.98 m2/s رسم شده است. شکل منحنى (منحنى انرژى مخصوص به ازاء مقدار ثابت دبي) داراى دو مجانب است يکى خط y=0 و ديگرى خط y=E به ازاء هر مقدار از E دو مقدار براى y بهدست مىآيد و تنها در يک نقطه است که به ازاء E فقط يک مقدار براى آن وجود دارد و آن حداقل انرژى مخصوص يا Emin است. عمق جريان را در زمانى که انرژى مخصوص حداقل است عمق بحرانى گويند (yc). در ساير مقادير E دو عمق براى جريان وجود خواهد داشت يکى از اين عمقها کوچکتر از yc و ديگرى بزرگتر از yc است. چنانچه عمق جريان کوچکتر از عمق بحرانى باشد جريان را از نوع فوق بحرانى (ysup) و اگر عمق جريان بزرگتر از عمق بحرانى باشد آن را زيربحرانى (usub) گويند.
|
|
|
|
|
| حال مفهوم انرژى مخصوص را در يک سيستم جريان آب درآبراهه روباز که در شکل (مثالى از کاربرد مفهوم انرژى مخصوص در جريان آب در يک آبراهه مستطيلى که کف آن در يک نقطه پلکانى است) آب در يک کانال مستطيلى که کف آن افقى است جريان دارد. درقسمتى از کانال سکوئى تعبيه شده است که به آن حالت پلکانى مىدهد. ارتفاع اين سکو ΔZ و مقدرا دبى در واحد عرض q است. دو نقطه ۱ و۲ را دو طرف سکو در نظر مىگيريم. فرض کنيم افت انرژى در سکو و بين مقاطع ۱ و ۲ ناچيز و بار کل ثابت و بهمقدار H باشد. همچننى فرض مىشود با توجه به انرژى مخصوص عمق جريان بالاتر از عمق بحرانى و رژيم حالت زيربحرانى دارد بر اساس معادله برنولى داريم:
|
|
| (معادله ۲۱): |
Z1 + y1 + (v1)2/2g = (Z1+∆Z) + y2 + (v2)2/2g |
|
|
| چنانچه بهجاى v مقدار معادل آن را برحسب دبى و عمق بنويسيم:
|
|
| (معادله ۲۲): |
Z1 + y1 + (q2)/2g(y1)2 = (Z1+∆Z) + y2 + (q2)/2g(y2)2 |
|
|
| که بهصورت زير حلاصه مىشود:
|
|
| (معادله ۲۳): |
H = Z1 + E1 = (Z1+∆Z) + E2 |
|
|
| و انرژى مخصوص در مقطع ۲ برابراست با:
|
|
| (معادله ۲۴): |
E2 = E1 - ∆Z |
|
|
| و چون جريان زير بحرانى است و ما در نيمه بالائى منحنى انرژى مخصوص کار مىکنيم لذا:
|
|
| |
|
| بنابراين پس از سکو عمق جريان کاهش مىيابد که اگر بخواهيم مقدار y2 را بهدست آوريم بايد بهروش آزمون و خطا يک معادله درجه ۳ را حل کنيم.
|
|
|
|