|
|
حافظهٔ کوتاهمدت بهمثابهٔ حافظهٔ فعال (working memory)
|
|
| حافظهٔ کوتاهمدت نقش مهمی در تفکر دارد. وقتی هوشیارانه میکوشیم مسئلهای را حل کنیم، حافظهٔ کوتاهمدت، فضای کار ذهنی را تشکیل میدهد: یعنی جائی است برای ذخیرهسازی عناصر مسئله و همچنین اطلاعات دریافتی از حافظهٔ درازمدت دربارهٔ آن مسئله. برای مثال، در نظر بگیرید که هنگام ضرب عدد ۳۵ در عدد ۸ در ذهن شما چه میگذرد: حافظهٔ کوتاهمدت باید این دو عدد (۳۵ و ۸)، ماهیت عمل ریاضی لازم (ضرب)، و عملیات حساب نظیر ۴۰=۵ × ۸ و ۲۴۰=۳۰ × ۸ را ذخیره کند. اگر همزمان با عملیات ذهنی حساب بخواهیم کلمات یا ارقامی را نیز بهخاطر بسپاریم، بیشک کارآئی ما در محاسبات لطمه میبیند. برای مثال، سعی کنید ضمن بهخاطر سپردن شمارهٔ تلفن ۱۷۳۹-۷۴۵ عملیات یادشده را انجام دهید (بادلی و هیچ - Hitch در ۱۹۷۴). بهخاطر نقشی که حافظهٔ کوتاهمدت در محاسبات ذهنی دارد، پژوهشگران بیش از پیش مایل هستند آن را 'حافظهٔ فعال' بنامند، و به آن همانند نوعی تخته سیاه بنگرند که ذهن محاسبات خود را روی آن انجام میدهد و نتایج میانی را برای استفادهٔ بعدی برروی آن مینویسد (بادلی، ۱۹۸۶).
|
|
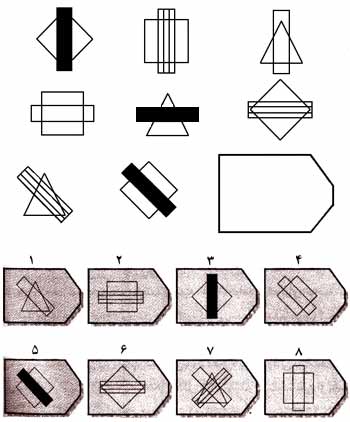
| پژوهشهای دیگری نشان میدهند که حافظهٔ کوتاهمدت نهتنها در حل مسائل عددی، بلکه در حل تمامی انواع مسائل پیچیده نیز در کار است. نوعی از این مسئلهها قیاسهای هندسی است که گاهی در آزمونهای هوش نیز بهکار میرود (مثلاً آزمون ریون - Raven در ۱۹۵۵). نمونهای از این قیاسهای هندسی را در شکل نمونهای از قیاسهای هندسی میبینید. سعی کنید آن را حل کنید تا نقش حافظهٔ کوتاهمدت را در حل مسئله تجربه کنید. شاید متوجه شوید که در این کار در دو مورد زیر برای ذخیرهسازی به حافظهٔ فعال نیاز دارید:
|
|
| ۱. شباهتها و تفاوتهائی که در شکلهای یک ردیف میبینید.
|
| ۲. قواعدی که برای توجیه این شباهتها و تفاوتها پیدا میکنید و آنها را برای انتخاب پاسخ درست بهکار میبندید.
|
|
| مسلماً هرچه گنجایش حافظهٔ فعال کسی بیشتر باشد، در مسائلی مانند این مسئله بهتر عمل خواهد کرد. (البته از لحاظ گنجایش حافظهٔ فعال، تفاوت نسبتاً اندکی بین آدمها دیده میشود.) علاوه بر این، وقتی برنامههای رایانهای برای شبیهسازی حل مسئله در انسان (از قبیل مسئلهٔ شکل نمونهای از قیاسهای هندسی) نوشته میشود، یکی از مهمترین عوامل تعیینکنندهٔ کارآئی آنها گنجایش حافظهٔ فعال است که برنامهریز آن را پیشبینی کرده است. تردیدی نیست که دشواری بسیاری از مسائل پیچیده تاحدودی بهخاطر باری است که این مسائل بر حافظهٔ فعال تحمیل میکنند (کارپنتر - Carpenter، جاست - Just و شل - Shell در ۱۹۹۰).
|
|
| نقشی که حافظهٔ کوتاهمدت یا فعال در فهم زبان ایفاء میکند پیچیدهتر است. ظاهراً نظام حافظهٔ کوتاهمدت که شرح آن گذشت در فهم جملههای نسبتاً ساده دخالت ندارد. گویاترین شواهد در این زمینه از بررسی بیماران آسیبدیدهٔ مغزی مبتلا به اختلال حافظه بهدست آمده است. وقتی فهرستی از واژههای فاقد ارتباط با یکدیگر به این بیماران عرضه میشود، برخی تنها میتوانند یک کلمه را تکرار کنند (فراخنای حافظهٔ آنها ۱ است)، اما وقتی جملهٔ کاملی به آنها ارائه شود، قادر هستند تمام جمله را تکرار کنند. برعکس، بیماران آسیبدیدهٔ مغزی دیگری از فراخنای حافظهٔ بهنجار برخوردار هستند، اما قادر نیستند جملهٔ سادهای را تکرار کنند. این یافتهها حاکی از آن است که در پردازش زبان، نظام ویژهای در کار است. بیماری که مشکلی در فراخنای حافظه دارد اما از نظر فهم زبان طبیعی است، میتوان گفت حافظهٔ کوتاهمدتش دچار اختلال است اما حافظهٔ زبانی بهنجار دارد. عکس این وضعیت در بیماری دیده میشود که فراخنای حافظهاش طبیعی است اما در فهم زبان کاستی دارد. حافظهٔ ویژهٔ زبان ظاهراً محدود به جملههای نسبتاً ساده است. در جملههای پیچیده از قبیل 'فروشندهای که پزشک معاینهاش کرد، رفته است' ، حافظهٔ کوتاهمدت بهکمک میآید. از اینرو، در فهم جملهها حافظهٔ کوتاهمدت در نقش پشتیبان حافظهٔ درازمدت عمل میکند (مککارتی - McCarthy و وارینگتون - Warrington در ۱۹۸۷).
|
|
| بهنظر میرسد در سطوح بالاتر فرآیندهای زبانی، نظیر گفتگو با کسی یا خواندن متنی، حافظهٔ کوتاهمدت نقش اصلی داشته باشد. وقتی هدف از خواندن مطلبی فهم معنی آن باشد، باید آگاهانه جملههای تازه را بهبرخی مطالب قبلی ارتباط داد. این پیونددادن مطلب تازه به مطالب قبلی ظاهراً در حافظهٔ کوتاهمدت صورت میگیرد، زیرا ثابت شده است کسانی که گنجایش حافظهٔ کوتاهمدتشان بیشتر است در آزمونهای درک خواندن نیز نمرههای بالاتری دارند (جاست و کارپنتر، ۱۹۹۲؛ دینمن - Daneman و کارپنتر، ۱۹۸۰).
|
|
|
|
|
| تکلیف آزمودنی این است که شکلهای ماتریس ۳ × ۳ را که در آن، شکل سمت راست ردیف سوم افتاده است در نظر بگیرد، و بعد بگوید کدامیک از هشت شکل داده شده در دو ردیف زیرین باید در جای خالی قرار گیرد. برای اینکار، آزمودنی بایستی بههر ردیف دقت کند، سپس قاعدهٔ تغییر شکلها را پیدا کند و همینکار را در مورد هر ستون نیز انجام دهد (اقتباس از کارپنتر، جاست و شل، ۱۹۹۰).
|