شنبه, ۴ اسفند, ۱۴۰۳ / 22 February, 2025
مجله ویستا
تغییرات رشد(Growth dynamics)
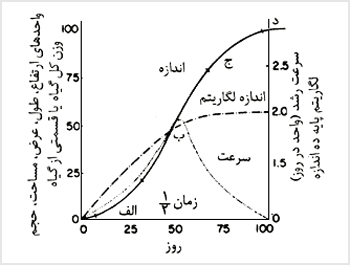
| الگوى رشد در طى يک سال نوعاً بهوسيلهٔ يک تابع رشد که موسوم به منحنى سيگموئيدى است مشخص مىشود. چارچوب زماني، بسته به اندام يا عضو ممکن است از کمتر از چند روز تا چند سال تغيير نمايد ولى الگوى تجمعى سيگموئيدى نمايانگر رشد تمام اندامها، اعضاء، بافتها و حتى اجزاء سلول مىباشد. اگر وزن گياه (ماده خشک)، حجم، سطح برگ، ارتفاع يا تجمع مواد شيميائى را نسبت به زمان رسم کنيم، خطى که اعداد را بههم وصل مىکند بهطور طبيعى سيگموئيدى خواهد بود (نمودار خطوط منحنىهاى تعميم يافته براى اندازه و... سرعت رشد که نسبت به زمان رسم شدهاند). منحنى S شکل، از سرعتهاى مختلف رشد در طول سيکل زندگى نتيجه مىشود. براى مثال رشد گياهچه آهسته بوده و معمولاً وزن مادهٔ خشک در طى يک دوره کوتاه يک يا دو هفتهاى کاهش مىيابد. بهدنبال اين مرحله دورهاى از رشد تصاعدى (قسمت الف و در شکل A)، آغاز مىشود. | ||||
| اين مرحلهٔ تصاعدى در جامعهٔ گياهى محصولات زراعي، نسبتاً کوتاه است. بهدنبال آن مرحلهٔ خطى (ب) آغاز مىشود که در طى آن ماده خشک با سرعت ثابتى افزايش مىيابد و براى يک دوره نسبتاً طولانى ادامه دارد. در وضع سبز گياهان، مرحلهٔ خطى توصيفى از سرعت رشد محصول (CGR)، مىباشد. CGR ساقهها و قسمتهاى ديگر ممکن است به ميزان کمترى با شروع شکلگيرى دانه و بهعلت کاهش وزن ساقهها که حاصل حرکت و توزيع مجدد ذخاير غذائى ناپايدار به بذرها است، منفى مىشود. اصل توزيع دوباره مواد فتوسنتزى از ساختمانهاى رويشى به زايشى در شکل B نشان داده شده است. سرعت خطى با يک مرحله کاهش سرعت رشد (ج) دنبال مىشود و بهعبارت ديگر افزايش رشد بسته به زمان تا رسيدن به يک حالت ثابت بهطور تصاعدى کم مىشود (د) اين مرحلهٔ 'بلوغ' يا 'رسيدگى فيزيولوژيکي' ناميده مىشود. در اين مرحله افزايش حاصله (براى مثال در ماده خشک) با تلفات در حال تعادل هستند. | ||||
| ||||
| ||||
| جنبههاى کمى رشد اغلب با مطالعهٔ اعضاء تکسلولى مثل مخمر يا گياهان کوچک از قبيل عدسک آبى (Lemna sP)، مىتواند بهتر مجسم شود. با فرض عدم محدوديت محيطى تعداد سلولها يا عدسک مىتواند بهصورت زير بعد از نسل اول تخيم زده شود: | ||||
| ||||
| در اين فرمول N۱ = تعداد تکسلولىها يا عدسک و N۰ = تعداد اوليه سلولها يا عدسک مىباشد. بدين صورت در پايان نسل اول دو سلول يا عدسک جايگزين يک سلول شدهاند. تعداد سلولها در پايان نسل دوم چنين است: | ||||
| ||||
| و تعداد آنها در پايان نسل سوم با شروع يک تکسلولى يا عدسک چنين است: | ||||
| ||||
| تعداد سلولها در پايان نسل nام چنين خواهد بود. | ||||
| ||||
| اگر فاصلهٔ زمانى بين نسلها نسبتاً ثابت باشد (همانطورى که معمولاً حقيقت دارد) معادله مىتواند بدين صورت نوشته شود: | ||||
| ||||
| در اين فرمول e پايهٔ لگاريتم طبيعي، k عدد ثابت براى سرعت رشد و t زمان است. تابع سرعت رشد بهجاى خطي، تصاعدى يا لگاريتمى است و اغلب بهعنوان معادلهٔ ربح مرکب معروف است. اين فرمول تحت شرايط معينى براى گياهان پرسلولى يا عالى با جايگزين نمودن وزن بهجاى تعداد سلول بدين طريق بهکار برده مىشود: | ||||
| ||||
| در اين فرمول W وزن و r مقدار ثابت سرعت رشد (نرخ بهره) است. | ||||
| رشد در گياهان تکسلولى و گياهان عالى وقتى که رقابت (مثلاً براى فضا، مواد مصرفي، يا عناصر غذائي) وجود داشته باشد نمىتواند با يک سرعت تصاعدى دوام داشته باشد. مرحلهٔ رشد تصاعدى در محصولات زراعى بهخصوص در تراکم زياد ممکن است فقط چند رزو دوام داشته باشد. حتى در گياهان فاصلهدار، رقابت درونى يا بعضى محدوديتهاى ديگر، سرعت تصاعدى را پايان داده و سرعت خطى را برقرار مىنمايد. وقتى پوشش گياهى بسته شود، سرعت رشد تا هنگام پيري، خطى بوده و در نهايت سرعت را به صفر يا يک حالت ثابتى مىکاهد. | ||||
| بسيارى از متخصصان زراعت مرحله رشد تصاعدى را بهعلت اينکه کوتاهمدت و در مرحلهٔ جوانى گياه مىباشد اهميت کمى براى آن قائل هستند. دوام و ضريب زاويه (درصد) مرحلهٔ رشد خطى (شکل A ب و ج) به بهترين وجهى عملکرد را توجيه مىکنند. رشد خطى با معادلهٔ a + bx بيان شده است در اينجا a محل تقاطع محور y و b شيب (سرعت) بهازاء هر واحد x است. |
همچنین مشاهده کنید
ایران مسعود پزشکیان دولت چهاردهم پزشکیان مجلس شورای اسلامی محمدرضا عارف دولت مجلس کابینه دولت چهاردهم اسماعیل هنیه کابینه پزشکیان محمدجواد ظریف
پیاده روی اربعین تهران عراق پلیس تصادف هواشناسی شهرداری تهران سرقت بازنشستگان قتل آموزش و پرورش دستگیری
ایران خودرو خودرو وام قیمت طلا قیمت دلار قیمت خودرو بانک مرکزی برق بازار خودرو بورس بازار سرمایه قیمت سکه
میراث فرهنگی میدان آزادی سینما رهبر انقلاب بیتا فرهی وزارت فرهنگ و ارشاد اسلامی سینمای ایران تلویزیون کتاب تئاتر موسیقی
وزارت علوم تحقیقات و فناوری آزمون
رژیم صهیونیستی غزه روسیه حماس آمریکا فلسطین جنگ غزه اوکراین حزب الله لبنان دونالد ترامپ طوفان الاقصی ترکیه
پرسپولیس فوتبال ذوب آهن لیگ برتر استقلال لیگ برتر ایران المپیک المپیک 2024 پاریس رئال مادرید لیگ برتر فوتبال ایران مهدی تاج باشگاه پرسپولیس
هوش مصنوعی فناوری سامسونگ ایلان ماسک گوگل تلگرام گوشی ستار هاشمی مریخ روزنامه
فشار خون آلزایمر رژیم غذایی مغز دیابت چاقی افسردگی سلامت پوست