تعادل(Equilibrium)

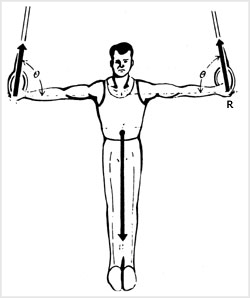
وقتى جسمى در حال سکون باشد و در آن هيچ‌گونه حرکت انتقالى و يا چرخشى ديده نشود گفته مى‌شود آن جسم در حال تعادل است. ژيمناستى که روى دارحلقه، حرکت صليب را نشان مى‌دهد (شکل زير) مى‌تواند مثال مناسبى براى نشان دادن ويژگى‌هاى تعادل باشد. بدن ژيمناست در اين حرکت تحت تأثير سه نيروى خارجى قرار گرفته است. F و 'F دو نيرويى هستند که به‌وسيلهٔ حلقه‌ها بر بدن او وارد شده و در زاويهٔ θ نسبت به سطح افقى عمل مى‌کنند و نيروى سوم وزن بدن او مى‌باشد که به عبارت ديگر آن را نيروى گرانش مى‌ناميم.

براساس اطلاعات مندرج در تصوير فوق مى‌توان برآيند نيروها را در هر جهت محاسبه نمود:

F_R sinθ + F_L sinθ-W = برآيند نيروى عمودى

F_R cosθ - F_L cosθ = برآيند نيروى افقي

فرض کنيم برآيند عمودى داراى ارزشى مثبت باشد بنابراين طبق قانون دوم نيوتن بديهى است که بدن ژيمناست در اثر نيرويى که به طرف بالا بر آن وارد مى‌شود متمايل به آن جهت است، برعکس اگر برآيند نيروى عمودى داراى ارزش منفى باشد تمايل حرکت برعکس به طرف پائين خواهد بود. اين هر دو شق نمى‌توانند قابل قبول باشند، زيرا واقعى نيستند و بدن ورزشکار ابداً تمايلى به بالا و پايين رفتن ندارد و لذا در صورتى که برآيند نيروى عمودى نتواند منفى و يا مثبت باشد ناگزير بايد نتيجه‌گيرى کنيم که مقدار آن بايد برابر با صفر باشد. همين دليل و منطق را مى‌توان در مورد برآيند نيروى افقى به‌کار برد و چنين نتيجه گرفت که مقدار آن برابر با صفر مى‌باشد و نهايتاً چون اولين ويژگى يک جسم در حال تعادل آن است برآيند مؤلفه‌هاى نيرو در هر جهت بايد برابر صفر باشد.

اطلاعات مندرج در شکل فوق نيز اجازه مى‌دهد تا برآيند نيروى چرخشى حول هريک از نقاط A، و B و C را در صفحهٔ مخصوص خود محاسبه نمود.

(F_L sinθ×d)-(W×d/2) = A برآيند نيروى چرخشى حول نقطهٔ

(F_r sinθ×d)-(W×d/2) = B برآيند نيروى چرخشى حول نقطهٔ

(F_L sinθ×d/2)-(F_rsinθ×d/2) = C برآيند نيروى چرخشى حول نقطهٔ

هرگاه ارزش عددى هريک از نيروهاى چرخشى سه‌گانهٔ فوق مثبت و يا منفى و به‌عبارت ديگر برابر صفر نباشد ژيمناست حُول محورى که از آن نقطه مى‌گذرد خواهد چرخيد. ليکن ما مى‌دانيم که ژيمناست در وضعيت صليب اصلاً نمى‌چرخد بنابراين نتيجهٔ نيروهاى مشروحهٔ فوق همگى برابر با صفر خواهد بود و مى‌توان چنين نتيجه گرفت که دومين مشخصهٔ يک جسم در حال تعادل آن است که برآيند گشتاور در يک صفحه و حول هر نقطه برابر با صفر خواهد بود. حال وقتى جسمى به اين شکل در حال تعادل و سکون باشد مى‌توان روى نيروهاى ناشناخته کار کرد و مقدار هريک از آنها را پيدا نمود. فرض کنيد که ژيمناست در تصوير فوق داراى وزنى برابر با ۱۵۰ پوند باشد و زاويهٔ ۷۵=θ درجه و فاصلهٔ d برابر با ۶ فوت باشد حال براى محاسبهٔ نيروى چرخشى حول نقطهٔ A مى‌توان چنين نوشت:

(F_L sinθ ×d₂)-(W×d/1)=0

(F_L sin ۷۵×۱۶)-(۱۵۰×۳)=۰

F_L=۴۵۰/(۶×۰.۹۶۶)=۷۷.۶۴ پوند

با اين عمل خودبخود مقدار FR نيز بديهى و روشن مى‌شود اما جهت تائيد مطلب مى‌توان همين عمل را حول نقطهٔ B و يا C محاسبه کرد. دربارهٔ اين نيرو در نقطهٔ B مى‌توان چنين نوشت:

F_R cosθ - F_L cosθ=0

F_R=F_l cosθ/cosθ=۷۷.۶۴ پوند

مؤلفه‌هاى داخلى و بالايى نيروهاى وارد بر دست‌هاى ژيمناست توسط حلقه‌ها به ترتيب برابر با F cosθ=۲۰.۱۱ پوند و Fsinθ=۷۵ پوند خواهد بود که دومى نشان مى‌دهد وزن بدن ژيمناست به‌طور تساوى توسط دو حلقه حمايت و نگهدارى مى‌شود. اين امر واقعيتى است که بيانگر تشابه وضع بدن ژيمناست روى دو حلقه مى‌باشد.

تغيير وضعيت‌هاى مختلف دربارهٔ تعادل غالباً براى اين منظور استفاده مى‌شود تا بتوان نيروى لازم بارى اختلال و بهم زدن تعادل را در اجسام محاسبه نمود. به‌طور مثال در ساختمان يک مانع دو و ميدانى قوانين بين‌المللى مى‌گويد مانع بايد طورى ساخته شود تا صورتى که نيروى حداقل برابر با ۶/۳ کيلوگرم (۸ پوند) و حداکثر برابر با ۴ کيلوگرم (۸ پوند و ۱۳ اونس) به مرکز لبهٔ فوقانى آن برخورد کند براى بهم زدن تعادل و انداختن آن کافى باشد. حال براى جلوگيرى از سرنگونى موانعى که با کمتر از نيرويى برابر با ۸ پوند واژگون مى‌شوند وزنه‌اى مخالف آن نيرو به پايه‌هاى مانع اضافه مى‌گردد.