یک مدل نظری از انقباض عضله بر مبنای سیستم های با فعالیت خود به خود

در این مقاله یک مدل نظری جدید برای تشکیل cross bridge ها در عضله ارائه شده و حرکت لغزان آن ها به وسیله شبیه سازی های کامپیوتری مورد بررسی قرار گرفته است در سطح میکروسکوپی , دینامیک های تولید شده در هر cross bridge چه به صورت پریودیک و چه آشوبگونه , از طریق لغزش تولید شده و هموار هستند

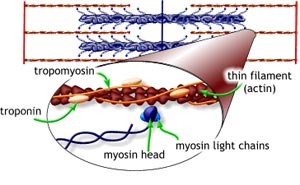
در این مقاله یک مدل نظری جدید برای تشکیل cross-bridge ها در عضله ارائه شده و حرکت لغزان آن ها به وسیله شبیه سازی های کامپیوتری مورد بررسی قرار گرفته است. در سطح میکروسکوپی ، دینامیک های تولید شده در هر cross-bridge چه به صورت پریودیک و چه آشوبگونه ، از طریق لغزش تولید شده و هموار هستند. در رابطه Hill’s شبیه سازی شده در دینامیک های کوچک وقتی سرعت حرکت بالاست ، نوسانات پریودیک غالب بوده و وقتی سرعت پایین است این نوسانات بیشتر به صورت آشوبگونه در می آیند. ماکسیمم بازدهی فرآیند تبدیل انرژی شیمیایی به مکانیکی در در گذر از نوسانات پریودیک به سمت نوسانات آشوبگونه به دست می آید.

● مقدمه

حرکت انقباضی فیبرهای عضلانی از فرآیند میکروسکوپیتبدیل انرژی شیمیایی به مکانیکی و تشکیل cross-bridge به وجود می آید. تاکنون دو نوع مختلف از تعاملات میکروسکوپی در فرآیند تشکیل cross-bridge ها پیشنهاد شده است. یکی کوپلینگ ناشی از تغییرات تطبیقی در ساختار ماکرومولکولی و دیگری کوپلینگ ضعیف ناشی از مشارکت نیروی جنبشی و تحریک حرارتی در بازچینی آماری در فاز دینامیک برای هر مولکول می باشد.

در این مقاله به وسیله تعمیم ایده Hulexy یک مدل دینامیک جدید ارائه شده که در آن فرآیند تشکیل cross-bridge ها به وسیله معادلات کاملا دترمینیسم شرح داده می شود. مدل مورد نظر بسیار بوده اما دو محدودیت اساسی دارد :

۱) یکی از آن ها محلی بودن ناحیه تعامل بین مولکول های اکتین و میوزین

۲) دیگری اثر زمان مقاوم است که طول پریود تعامل را در فرآیند تشکیل cross-bridge ها کنترل می کند. همان طور که در شکل (۱-a) نشان داده شده فیلامان میوزین به شکل یک میله غیر قابل انعاطاف بوده و سر آن (HMM) فقط وقتی با فیلامان اکتین در تعامل است که در محل های فعال قرار گیرد. این محل ها به صورت متناوب در سراسر فیلامان اکتین توزیع شده اند. وقتی که HMM از ناحیه فعال خارج شد ، مکانیسم تشکیل cross-bridge ها برای این پریود خاص مهار می گردد.

▪ شکل ۱.

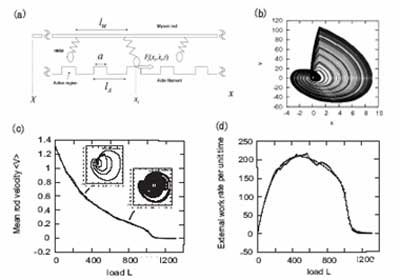
b) نوسانات آشوبگونه یک

cross-bridge . (c) رابطه Hill’s و انطباق آن بر روی منحنی تجربی

Edman . (d) بازدهی مربوط به منحنی شکل c . سمت چپ ماکسیمم بازدهی به نوسانات پریودیک و سمت راست آن ب نوسانات آشوبگونه مربوط است.

فرض کنید معادلات توصیف کننده حرکت در هر HMM ، xi ، و میوزین ، X ، به فیلامان اکتین با رابطه زیر ارتباط دارد :

m xi۰۳۹;۰۳۹; = −k(xi − X − (i − ۱)lA) − ۹۴۷; xi۰۳۹; + Fi(xi, xi۰۳۹;, t) , (i = ۱, ۲, • • •,N)

M X۰۳۹;۰۳۹; = ∑Ni=۱ k(xi − X − (i − ۱)lA) − ۹۵۰; X۰۳۹; − L ,

که در این رابطه (۹۴۷;, ۹۵۰;) ، ویسکوزیته ، L بار ، k الاستیسیته و (lM, a, lA) فضای هر المان می باشد. فرآیندتولید نیرو که با هیدرولیز مولکول های ATP همراه است به صورت زیر فرض می شود :

Fi(xi, xi۰۳۹;, t) = F۰ − ۹۴۵; (von(i) − ۹۴۶;)۲ , (t ~є refractory time ∩ xi active sites).

در این رابطه von(i) سرعت لحظه ای HMM را موقع شروع تولید نیروی Fi نشان داده و نماینده سرعت موثر در فرآیند تبدیل انرژی شیمیایی به مکانیکی می باشد. وقتی حرکت لغزنده میوزین به وسیله نیرو متوقف شد ، HMM دینامیک های غیرخطی پیچیده ای مثل نقطه ثابت ، سیکل حدی ، دوبرابر شدن پریود و آشوب را از خود نشان می دهد. شکل (۱-b) یک نمونه از نوسانات آشوبگونه را ر فضای فاز نشان می دهد. وقتی ما نیروی خارجی را حذف کنیم حرکت میوزین با یک سرعت مشخص صورت می گیرد که این سرعت به بار L بستگی نداشته و به پارامترهای دیگری مربوط است. رابطه V-L در شکل (۱-c) همان رابطه Hill’s مدل مورد نظر است که به خوبی بر روی منحنی تجربی Edman فیت شده است. این رابطه تک فاز نیست بلکه به صورت دوفازه است. نقاط برخورد دینامیک های کوچک در سرعت های بالا پریودیک و در سرعت های پایین آشوبگونه می باشد.

نسرین شعوری

مرجع

T.Mitsui , Y.Aizawa , " A Theoretical Model for Muscle Contraction based on Refractory-Activation Systems " , Department of Applied Physics, Faculty of Science and Engineering, Waseda University, Tokyo ,۲۰۰۶.