مرزبندی مناطق آبی ایران به كمك شاخص آشفتگی بارش

در ایران بارش یكی از متغیرهای اساسی برای ارزیابی مهیایی بالقوه منابع آب است

● چكیده

در این مقاله مقدار بارش ماهانه ۳۳۷۹۴ سال ـ ایستگاه که در مجموع شامل ۴۰۵۵۲۸ اندازه‌گیری بارش در ایستگاههای سینوپتیک، کلیماتولوژی و بارانسنجی ایران بوده به كمك نظریه آشفتگی شانون بررسی شده است. میزان عدم قطعیت تسهیم بارش در طول سال به كمك شاخص آشفتگی اندازه گیری شده و نقشه هم آشفتگی ایران ترسیم گردیده است. همچنین این نقشه آشفتگی با نقشه نواحی اقلیمی ایران مقایسه شد و مشخص شد كه شاخص آشفتگی توانایی بیان خصوصیات بارش كشور را دارد. با تركیب نقشه شاخص آشفتگی با نقشه بارش سالانه ایران امكان طبقه بندی كشور بر مبنای مهیایی بالقوه منابع آب فراهم گردید. بررسیها نشان داد در ایران چهار ناحیه مهیایی منابع آب وجود دارد.

۱) مقدمه

در ایران بارش یكی از متغیرهای اساسی برای ارزیابی مهیایی بالقوه منابع آب است. هر چند بارش سرشتی تناوبی دارد اما توزیع زمانی و مكانی آن بسیار ناموزون است و به همین دلیل توزیع منابع آب نیز از توزیع یكنواختی برخوردار نیست. نگهداری و مدیریت منابع آب، هم تابعی از بارش دریافتی است و هم به تغییر پذیری بارش بستگی دارد. هرچه تغییرات مكانی بارش كوچكتر باشد همگنی و یكدستی منابع آب بیشتر می شود.

از سوی دیگر هر چه تغییر پذیری زمانی بارش كمتر باشد منابع آب نیز با ثبات تر خواهد بود و عرضه دائمی آب امكان پذیر می شود. به همین دلیل تغییر پذیری زمانی بارش در ارزیابی مهیایی منابع‌آب‌آبخیزها ومطالعه مهیایی نسبی منابع آب در مقیاس محلی و منطقه‌ای اهمیت زیادی دارد.

نظریه آشفتگی (entropy theory) در ابتدا در زمینه ارزیابی كمی عدم قطعیت متغیرهای آب شناختی و در مورد مدلهای منابع آب و پارامترهای آنها بكار گرفته شد (هارمانجی اغلو وهمکاران ۱۹۹۲ ص ۹۸، سینگ ۱۹۹۷ ص ۵۹۵، هارمانجی اغلو و سینگ ۱۹۹۸ ص ۲۳۴) ولی ظاهراً تاكنون جز کاواچی و همکاران (۲۰۰۱ ص ۴۱) که از این شاخص برای مرزبندی نواحی آبی ژاپن استفاده کرده اند از این نظریه برای مرزبندی مناطق بارشی و به تبع آن ارزیابی منابع آب مناطق بزرگ استفاده نشده است.

کاسلتون و حسین (۱۹۸۰ ص ۵۱۲) از شاخص «بیشینه انتقال اطلاعات» برای انتخاب ایستگاه های هیدرومتری شبكه های آب سنجی استفاده كرده اند. حسین (۱۹۸۹ ص ۵۳۰) برای گزینش تعداد بهینه ای از ایستگاه‌های یك شبكه چگال از شاخص آشفتگی استفاده كرده است. ا و برای تقویت و گسترش شبكه های دیده بانی با استفاده از داده‌های شبكه تنك موجود و ترسیم نقشه هم آنتروپی، مناطقی كه دارای كمترین مقدار اطلاعات آب شناختی بوده اند را شناسایی كرده است. در یک تحقیق دیگر کرستانویچ و سینگ (a ۱۹۹۲ ص ۱۶۱) انتقال اطلاعات مابین چند دوره خشكسالی و سیل متوالی را در یك سری زمانی طولانی بارش ماهانه به كمك شاخص های مختلفی از جمله شاخص آشفتگی كرانه ای، آشفتگی مشترك و شاخص «انتقال اطلاعات» (information transmission) بررسی كرده اند.

در تحقیقی دیگر کرستانویچ و سینگ (b ۱۹۹۲ ص ۲۸۱) و همچنین کرستانویچ و سینگ (c ۱۹۹۲ ص ۳۱۲) به كمك شاخص انتقال اطلاعات كاربرد نظریه آشفتگی را در ارزیابی تغییرات زمانی مكانی بارش و بسند گی تعداد ایستگاههای باران سنجی لوئیز یانا بررسی كرده اند. یانگ و برن (۱۹۹۴ ص ۳۱۲) بر مبنای شاخص آشفتگی روشی برای طراحی شبكه های دیده بانی ارائه كرده اند. مارویاما و کاواچی (۱۹۹۸ ص ۸) به كمك آشفتگی كرانه ای خصوصیات بارشهای محلی ژاپن را بررسی و ارزیابی كرده اند. غیور و مسعودیان(۱۳۷۵) برای ارزیابی اندازه یکنواختی توزیع زمانی بارش در ایران شاخص یکنواختی را ارائه کرده اند. این شاخص برخلاف شاخص آشفتگی از دو طرف بسته است و بین صفر تا صد تغییر می‌کند. اما در این بررسی ما چند هدف را دنبال می كنیم: یكی بررسی درجه تغییرپذیری (درجه عدم قطعیت وقوع بارش یا تسهیم زمانی بارش) الگوهای بارش ماهانه ایران، دوم مرزبندی پراكندگی آشفتگی بارش در ایران ، سوم مقابله نقشه آشفتگی بارش با نقشه نواحی اقلیمی ایران و چهارم تهیه یك نقشه مهیایی آب از راه تلفیق نقشه آشفتگی با نقشه بارش.

۲) آشفتگی بارش

۱ـ۲) شاخص آشفتگی اطلاعاتی شانون

شانون در سال ۱۹۴۸ نظریه آشفتگی اطلاعاتی را ارائه كرد و آشفتگی را به عنوان شاخص سنجش اطلاعات، گزینش یا عدم قطعیت بصورت زیر معرفی كرد:H= - k∑ pi log pi (۱)

در اینجاPi احتمال برآمد یك متغیر تصادفی گسسته، k یك مقدار ثابت مثبت و H شاخص آشفتگی متغیر تصادفی مورد نظر است. اگر K را برابر یك ولگاریتم را در پایه دو در نظر بگیریم فرمول یك به صورت زیر ساده می شود: (۲)

واحد این شاخص آشفتگی بیت است و n تعداد برآمدها یا رخدادهاست. اگر همه Pi ها برابر باشند یعنی Pi =۱/n آنگاه مقدار آشفتگی معادل H=log۲n خواهد بود. در این صورت H یك تابع صعودی یكنوا خواهد بود كه مقدار آن تابع n است. برای هر n دلخواه در صورتی كه همه Pi ها برابر باشند H بیشینه می شود. برعكس هرگاه همه Pi ها به جز یكی برابر صفر باشند H كمینه می شود. این بدان معناست كه همه برآمدهای متغیر تصادفی یكی هستند و تنها یكی ازPi ها معادل یك است. بنابراین مقدار آشفتگی بین صفر تا log۲n متغیر است و مقدار آن به شكل توزیع احتمالات Pi)ها( بستگی دارد. هر چه قیود (پارامترهای) توزیع احتمال بیشتر باشد، آشفتگی كاهش می یابد و بر عكس. از این لحاظ آشفتگی را می‌توان برآوردی از عدم قطعیت توزیع احتمال به شمار آورد.

۲ـ۲) شاخص آشفتگی و تسهیم زمانی بارش

با اینكه به كمك نظریه آشفتگی می توان عدم قطعیت سری های زمانی بارش را اندازه گیری كرد این عدم قطعیت هم به شدت بارش بستگی دارد و هم به دفعات وقوع بارش (تسهیم زمانی بارش). اما نظریه آشفتگی بیشتر برای تعیین عدم قطعیت شدت بارش یا مقدار بارش بكار رفته است. در اینجا احتمال (Pi)، عبارتست از فراوانی وقوع مقادیر گسسته بارش در یك دوره زمانی معین. مطابق این تعریف هرگاه بارش بطور كاملاً یكنواخت در زمان توزیع شده باشد شاخص آشفتگی برابر صفر می‌شود.

در اینجا می خواهیم عدم قطعیت تسهیم زمانی بارش را بررسی كرده و به كمك شاخص آشفتگی آنرا اندازه بگیریم. این شاخص مبتنی بر چگالی احتمال بارش و بر تسهیم تصادفی مقدار بارش بین قطعات زمانی معین استوار است كه به صورت زیر بدست می آید:

اول: سری زمانی بارش یك سال را در نظر بگیرید. فرض كنید ri كل مقدار بارش دریافتی در ماه iام سال باشد. مثلا r۱ بارش دریافتی ماه ژانویه و r۱۲ كل بارش دریافتی ماه دسامبر باشد. بدین ترتیب كل بارش دریافتی سالانه عبارتست از :(R = ri ) (۳)

مقدار ri می تواند صفر یا هر مقدار معین مثبتی باشد.

دوم: تغییرپذیری درون سالی بارش را با یك آزمون تصادفی تفسیر می كنیم. این آزمون مشتمل بر چندین تكرار است كه هر یك سرشتی احتمالاتی دارند. این آزمون به این شكل انجام می پذیرد كه اگر مثلاً بارش سالانه R برابر ۱۰۰ میلی متر باشد آنگاه آزمون دارای صد تكرار خواهد بود. اگر R اعشاری باشد آنرا به نزدیكترین عدد صحیح ناكوچكتر گرد می‌كنیم. هر تكرار شامل ۱۲ ماه است (از ژانویه تا دسامبر). در هر بار تكرار یكی از این ماهها به تصادف انتخاب می‌شود. به بیان دیگر احتمال انتخاب همه ماهها برابر است.

مقدار بارش ماه منتخب را برابر یك قرار می دهیم. مثلاً فرض كنید در تكرار اول، ماه ژانویه انتخاب شده باشد در این صورت بارش این ماه را برابر یك میلی متر قرار می دهیم. در تكرار دوم همین عمل انجام می گیرد یعنی یك ماه را به تصادف انتخاب كرده و مقدار بارش آنرا برابر یك میلی متر قرار می دهیم پس از انجام صد تكرار، مجموع بارش ماههای سال معادل ۱۰۰ میلی متر خواهد بود. اگر در جریان انتخاب تصادفی، یك ماه معین ده بار انتخاب شده باشد آنگاه مقدار بارش آن ماه معادل ۱۰ میلی متر یعنی تعداد دفعات انتخاب همان ماه خواهد بود. مقدار بارش ماههایی كه اصلاً انتخاب نشده اند برابر صفر خواهد بود. اگر مقادیر این سری زمانی را نسبت به ماههای سال ترسیم كنیم سری بارش سال بدست می آید. از روی این سری می توان مقدار بارش دریافتی ماه i ام یعنی r۱ تا rn را محاسبه كرده و سپس سری جدید را به R یعنی كل بارش سالانه تقسیم كرد و مقادیر Pi (فراوانی) را بدست آورد. (۴)

مقادیر فراوانی نسبی Pi كه به این ترتیب بدست می آیند مبین احتمال وقوع بارش در ماه i ام هستند و بنابراین توزیع آن معرف خصوصیت احتمالاتی تسهیم بارش سالانه در بین ماههای سال است. به بیان دیگر این سری عدم قطعیت وقوع بارش را اندازه می گیرد. با جایگذاری معادله ۴ در معادله ۲داریم. (۵)

از این معادله برای محاسبه آشفتگی بارش ایران استفاده شد. این معادله نشان می دهد كه مقدار H به ترتیب ri در سری بستگی ندارد و اگر كل بارش سال R تنها در یك ماه ببارد مقدار H برابر صفر خواهد شد و اگر R/n بطور یكنواخت در تمام طول سال توزیع شده باشد H بیشینه می شود. (Log۲n). به بیان دیگر هر چه H بزرگتر باشد تسهیم بارش یكنواخت تر است و تغییرپذیری زمانی بارش كمتر است.

بنابراین H معیاری نرده ای از تغییرپذیری بارش است. توجه دارید شاخصی كه در اینجا تعریف كردیم مبتنی بر مقدار بارش است و با شاخص تغییرپذیری كه مؤلفه ای برداری است و مبتنی بر زمان وقوع بارش است و خصوصیت فصلی رویدادهای آب شناختی (مانند سیل، بارش، خشكسالی و...) را می سنجد تفاوت دارد (ماگیلیگان و کرابر، ۱۹۹۶ : ۱۶۳ و برن، ۱۹۹۷ : ۲۱۸). اگر مقادیر بارش ماهانه چندین سال متوالی m برای یك ایستگاه دیده بانی در دست باشد میانگین شاخص آشفتگی كه بصورت زیر بدست میآید قابل محاسبه است :(۶)

۳) روش شناسی

۱ـ۳) داده های بارش

هم اکنون در ایران حدود ۱۸۰۰ ایستگاه دیده بانی وجود دارد كه هسته مركزی شبكه دیده بانی بارش ایران را تشكیل می دهند؛ هرچند داده های بارش ماهانه همه این ایستگاه ها از سال ۱۹۵۱ تا ۱۹۹۹ به مدت ۴۹ سال موجود نیست. به بیان دیگر یا دوره آماری برخی از ایستگاهها بسیار كوتاه است یا نقص آماری دارند. برای بدست آوردن مقداری قابل قبول برای روش زیر را بکار گرفتیم:

الف) نیمپراشنگار هر یک از ماههای سال بین سال ۱۹۵۱ تا ۱۹۹۹ برای ارزیابی رفتار مکانی بارش ماهانه ترسیم و بررسی شد.

ب) بر پایه بررسی مرحله الف یک شبکه با یاخته های ۱۵ کیلو متر در ۱۵ کیلومتر بر روی ایران گسترش داده شد.

ج) برای هرماه مقدار بارش گره های شبکه یاد شده به کمک همه ایستگاههایی که در ماه مورد نظر دارای اندازه گیری بوده اند به روش میانیابی کریگینگ و در مواردی که معادلات کریگینگ بی جواب بود از روش عکس فاصله با توان دو برآورد گردید.

د) برآوردهای روی گره ها به سری زمانی بارش هر گره تبدیل شد و مقدار شاخص آشفتگی هر سال به کمک رابطه ۵ محاسبه شد.

ه) مقدار متوسط شاخص آشفتگی برای هر گره به کمک رابطه ۶ محاسبه و نقشه هم آشفتگی ایران ترسیم شد.

۲ـ۳) محاسبه آشفتگی بارش

تغییرپذیری بارش بـه كمك شاخص آشفتگی اندازه‌گیـری شد. بـرای تبیین خصوصیات

توزیع بارش در طول سال داده های بارش ماهانه بررسی گردید. مقادیر بارش ماهانه به مقادیر توزیع احتمال وقوع بارش تبدیل شد و شاخص آشفتگی شانون برای هر سال در هر گره محاسبه شد (شانون، ۱۹۴۸، ص۶۳۰) سپس میانگین این شاخص برای هر گره بدست آمد. در مرحله بعد با استفاده از مقادیر شاخص آشفتگی یك نقشه هم آشفتگی برای ایران ترسیم شد.

شکل۱: میانگین شاخص آشفتگی بارش ماهانه بر روی گره‌ها

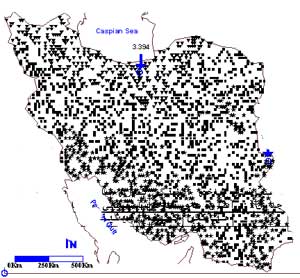
۱ـ۴) پهنه بندی نواحی آبی

شكل ۱ میانگین سالانه H را روی گره ها نشان می دهد. در جدول ۱ مقادیر میانگین، كمینه، بیشینه، انحراف معیار و تغییرپذیری H و R آمده است. مقدار شاخص آشفتگی بین ۸۵۸/۱ تا ۳۹۴/۳ متغیر بوده است.

همچنانكه شكل ۱ هم نشان می دهد شاخص آشفتگی، ایران را به چند منطقه متمایز تقسیم می‌كند. محاسبه تغییرپذیری بارش ماهانه از همان روشی استفاده كردیم كه برای محاسبه شاخص آشفتگی انجام داده بودیم.

▪ جدول۱: آماره‌های شاخص آشفتگی و بارش ایران

میانگین/ کمینه/ بیشینه/ انحراف‌معیار/ تغییرپذیری

آشفتگی (بیت)/ ۷۷۶/۲/ ۸۵۸/۱/ ۳۹۴/۳/ ۲۴۱/۰/ ۰۸۶۸/۰

بارش(میلیمتردرسال)/ ۴/۲۵۲/ ۸/۲/ ۱۸۶۳/ ۰/۱۹۶/ ۷۷۶/۰

/

سید ابوالفضل مسعودیان

منابع

۱ـ غیور، حسنعلی و مسعودیان، سید ابوالفضل، بررسی مکانی شاخص یکنواختی بارش ماهانه در ایران، فصلنامه تحقیقات جغرافیائی، شماره ۵۶، صفحه ۲۹ـ۱۹، ۱۳۷۵.

۲ـ مسعودیان، سید ابوالفضل، تحلیل خوشه ای بارش ماهانه ایران، طرح پژوهشی شماره ۸۱۰۳۰۵، معاونت پژوهشی دانشگاه اصفهان، ۱۳۸۲.

۳. Burn, D. H. (۱۹۹۷). Catchment similarity for regional flood frequency analysis using seasonality measures. Journal of Hydrology ۲۰۲, pp. ۲۱۲–۲۳۰.

۴. Caselton, W.F. and Husain, T. (۱۹۸۰). Hydrological networks: information transmission. Journal of Water Resources Planning and Management, ASCE ۱۰۶ WR ۲, pp. ۵۰۳–۵۲۰.

۵. Harmancioglu, N.B. and Singh, V. P. (۱۹۹۸). Entropy in environmental and water resources. In: Herschy, R.W. and Fairbridge, R.W., Editors, (۱۹۹۸). Encyclopedia of Hydrology and Water Resources, Kluwer Academic Publishers, Dordrecht, pp. ۲۲۵–۲۴۱.

۶. Harmancioglu, N.B., Singh, V.P. and Alpaslan, N. (۱۹۹۲). Versatile uses of the entropy concept in water resources. In: Singh, V.P. and Fiorentino, M., Editors, ۱۹۹۲. Entropy and Energy Dissipation in Water Resources, Kluwer Academic Publishers, Dordrecht, pp. ۹۱–۱۱۷.

۷. Husain, T. (۱۹۸۹). Hydrologic uncertainty measure and network design. Water Resources Bulletin ۲۵۳, pp. ۵۲۷–۵۳۴.

۸. Kawachi,T., T. Maruyama and VP Singh. (۲۰۰۱). Rainfall Entropy for Delineation of Water Resources Zones in Japan, Journal of Hydrology, ۲۴۶, pp.۳۶-۴۴.

۹. Krstanovic, P.F. and Singh, V.P. (۱۹۹۲). Transfer of information in monthly rainfall series of San Jose. In: Singh, V.P. and Fiorentino, M., Editors, ۱۹۹۲. Entropy and Energy Dissipation in Water Resources, Kluwer Academic Publishers, Dordrecht, pp. ۱۵۵–۱۷۳.

۱۰. Krstanovic, P.F. and Singh, V.P. (۱۹۹۲). Evaluation of rainfall networks using entropy I. Water Resources Management ۶, pp. ۲۷۹–۲۹۳.

۱۱. Krstanovic, P.F. and Singh, V.P. (۱۹۹۲). Evaluation of rainfall networks using entropy II. Water Resources Management ۶, pp. ۲۹۵–۳۱۴.

۱۲. Magilligan, F.J. and Graber, B.E. (۱۹۹۶). Hydroclimatological and geomorphic controls on the timing and spatial variability of floods in New England, USA. Journal of Hydrology ۱۷۸, pp. ۱۵۹–۱۸۰.

۱۳. Maruyama, T. and Kawachi, T. (۱۹۹۸). Evaluation of rainfall characteristics using entropy. Journal of Rainwater Catchment Systems ۴ ۱, pp. ۷–۱۰.

۱۴. Shannon, C.E. (۱۹۴۸). A mathematical theory of communication. The Bell System Technical Journal XXVII, pp. ۳۷۹–۴۲۳ see also ۶۲۳–۶۵۶.

۱۵. Singh, V.P. (۱۹۹۷). The use of entropy in hydrology and water resources. Hydrological Processes ۱۱, pp. ۵۸۷–۶۲۶.

۱۶. Yang, Y. and Burn, D.H. (۱۹۹۴). An entropy approach to data collection network design. Journal of Hydrology ۱۵۷, pp. ۳۰۷–۳۲۴.

---