یکشنبه, ۳۰ دی, ۱۴۰۳ / 19 January, 2025
شکلات؛ قضیه حمار
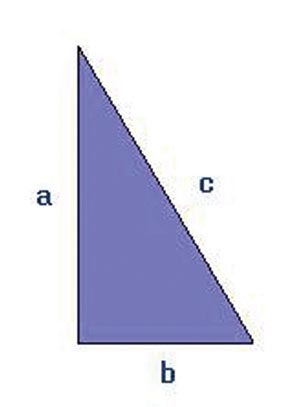
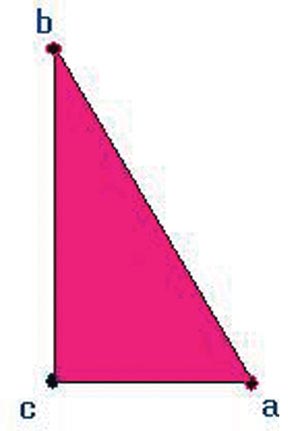
در ریاضی قضیه بسیار ساده و معروفی وجود دارد که میگوید در هر مثلث اندازه هر ضلع از مجموع اندازه دو ضلع دیگر کمتر و از تفاضل اندازه دوضلع دیگر بیشتر است.
یعنی اگر ضلعهای یک مثلث را a وb وc بنامیم، همواره خواهیم داشت:
a+b>c
a-b<c
دقت کنید که این قضیه تنها برای مثلث خاصی عنوان نشده است، اگر شما مثلثهای زیادی با اندازههای متفاوت بکشید، میبینید که جمع هر دو ضلع آن از ضلع دیگر بزرگتر و تفاضل هر دو ضلع آن از ضلع سوم کوچکتر است.اما اگر کمی دقت کنید میتوانید تعریف دیگری از این قضیه ارائه دهید. برای راهنمایی فرض کنید میخواهیم از نقطه a به نقطه b برویم.
به نظر شما کدام راه کوتاهتر است؟ کاملا واضح است که اگر یکسره از نقطه a به b برویم، مسافت کمتری را نسبت به زمانی که از a به c و سپس به bبرویم طی خواهیم کرد. این دقیقاً معادل همان چیزی است که نامساوی مثلث میگویند. به بیان دیگر کمترین فاصله بین دو نقطه خط راست است. جالب است بدانید که این قضیه به قضیه حمار شهرت دارد. چرا که گفته میشود اگر بوته علفی را در نقطه b قرار دهیم، یک الاغ که در نقطه aقرار دارد، همواره کوتاهترین مسیر را که همان وتر مثلث است برای رسیدن به آن پیش می گیرد!
آیدا ابوترابی
ایران مسعود پزشکیان دولت چهاردهم پزشکیان مجلس شورای اسلامی محمدرضا عارف دولت مجلس کابینه دولت چهاردهم اسماعیل هنیه کابینه پزشکیان محمدجواد ظریف
پیاده روی اربعین تهران عراق پلیس تصادف هواشناسی شهرداری تهران سرقت بازنشستگان قتل آموزش و پرورش دستگیری
ایران خودرو خودرو وام قیمت طلا قیمت دلار قیمت خودرو بانک مرکزی برق بازار خودرو بورس بازار سرمایه قیمت سکه
میراث فرهنگی میدان آزادی سینما رهبر انقلاب بیتا فرهی وزارت فرهنگ و ارشاد اسلامی سینمای ایران تلویزیون کتاب تئاتر موسیقی
وزارت علوم تحقیقات و فناوری آزمون
رژیم صهیونیستی غزه روسیه حماس آمریکا فلسطین جنگ غزه اوکراین حزب الله لبنان دونالد ترامپ طوفان الاقصی ترکیه
پرسپولیس فوتبال ذوب آهن لیگ برتر استقلال لیگ برتر ایران المپیک المپیک 2024 پاریس رئال مادرید لیگ برتر فوتبال ایران مهدی تاج باشگاه پرسپولیس
هوش مصنوعی فناوری سامسونگ ایلان ماسک گوگل تلگرام گوشی ستار هاشمی مریخ روزنامه
فشار خون آلزایمر رژیم غذایی مغز دیابت چاقی افسردگی سلامت پوست